En matematica se dice que una mangitud es función de otra magnitud si el valor de la primera depende del valor de la segunda.
Un ejemplo es cuando cargamos combustible, el PRECIO va a depender de los LITROS que carguemos.
Por lo tanto decimos, que el PRECIO esta en «FUNCIÓN» de la cantidad de LITROS que carguemos. Es decir el PRECIO depende de la cantidad comprada.
En matemáticas, las funciones se escriben a través de expresiones algebraicas. es decir utilizando letras y números a la misma vez.
Para escribir las magnitudes siempre usamos letras, las más comunes son X e Y.
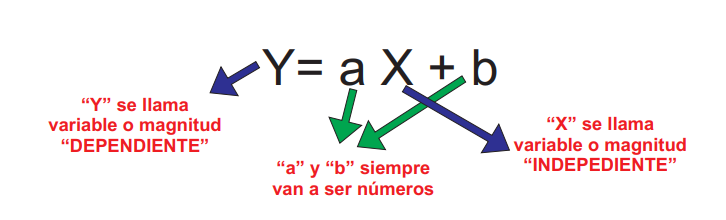
Ejemplo:
Y=3 X + 1
Esta expresión esta diciendo que: si a X la multiplico por 3 y luego le sumo 1 me va a dar el resultado de Y.
Toda función lineal va acompañada de una gráfica que va a ser una línea recta, de allí el nombre «función lineal».
Esa gráfica se va a dibujar en el plano usando como referencia dos lineas rectas que forman una cruz. Este sistema se lo llmará: «sistema de coordenadas cartesianas».
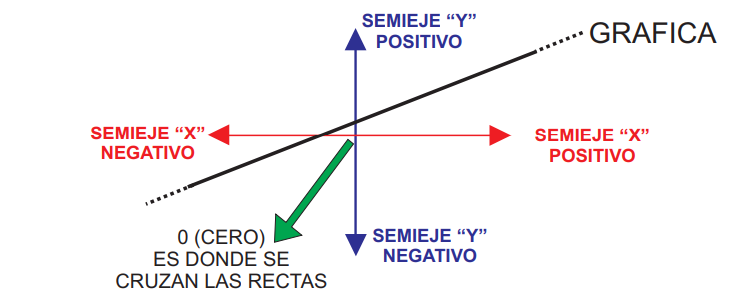
Ejemplo:
Se da la siguiente expresión y se nos pide que gráfiquemos:
Y = 2 X – 3
El primer paso:
Realizamos una tabla de valores para encontrar los valores de «Y» a partir de los valores de «X».

Los valores “X” al ser independientes le podemos dar el que querramos, generalmente usamos -2, -1, 0, -1, -2.
Luego esos valores lo reemplazamos en el lugar donde está la “X” en la expresión que nos dieron y encontramos el valor de “Y”, teniendo en cuenta de separar términos.
Una vez que encontramos el valor de “Y” para cada “X”, escribimos los pares ordenados que se generaron.
( -2, -7) Se llaman «par» porque son «dos números» y ordenado porque primero va el valor de «X» y luego el de «Y».
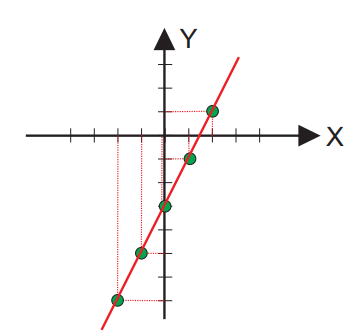
Las lineas punteadas de color rojo son las que no permiten unir el valor de «X», que generó el valor de «Y».
Los puntos verdes serian los pares ordenados que obtuvimos en la tabla.
La linea roja sería la grafica correspondiente a la expresión: Y = 2 X -3.
Función lineal: Gráfico sin tabla
Para poder graficar una pendiente sin tabla hay que tener en cuenta dos conceptos: Ordenada y Pendiente al origen.
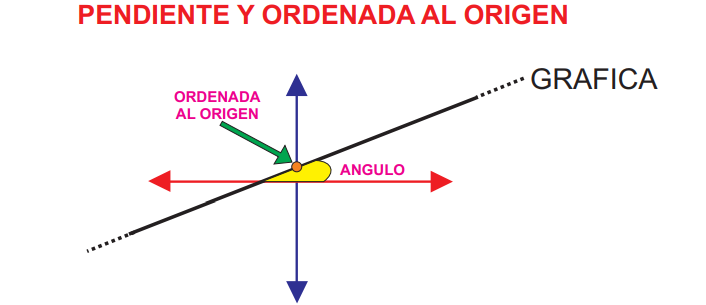
La PENDIENTE me indica la inclinación de la recta, es decir el ángulo que forma la gráfica con el eje “X”.
La ORDENADA AL ORIGEN me indica el punto que se origina cuando la gráfica se corta con el eje “Y”.
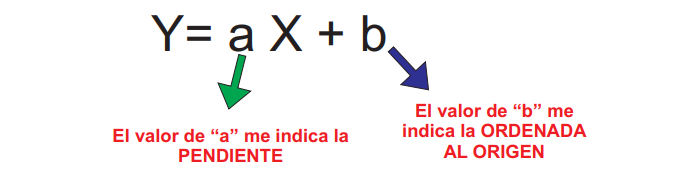
El valor de “a” siempre estará expresada como una fracción que nos indicará los movimientos verticales y horizontales que deberemos realizar.

Ejemplo:
Nos piden que grafiquemos la siguiente expresión:
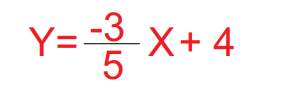
Primer paso: Identificamos la pendiente y la ordena al origen.
a= -3/5 (pendiente)
b= 4 (ordenada al origen)
Segundo paso: Marcamo en el sistema de Coordenadas, la ordenada al origen en el eje «Y».
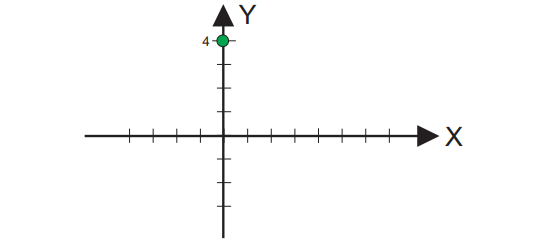
Tercer paso: a partir del punto marcado empezamos a marcar la pendiente.
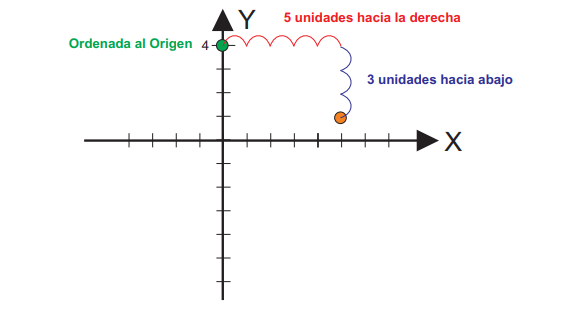
Cuarto paso: A partir de los dos puntos obtenidos marcamos la recta.
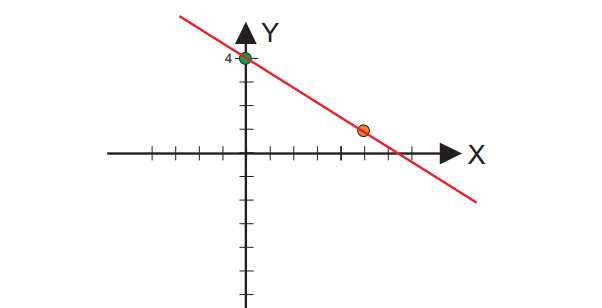
Para hacer el camino inverso, es decir si nos dan la grafica y debemos escribir la fórmula, se debe hacer lo siguiente:
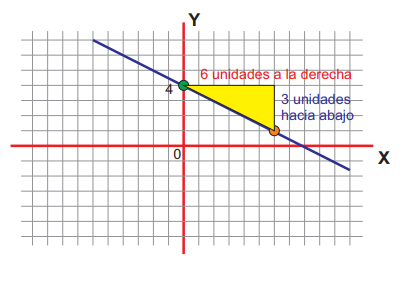
Nos fijamos el valor de la ordenada al origen (punto verde) en este caso b=4.
Luego vemos el camino para llegar al punto naranja, ese camino debe formar un triangulo con la gráfica (azul) y armamos la fórmula.

Función lineal: Rectas paralelelas y perpendiculares
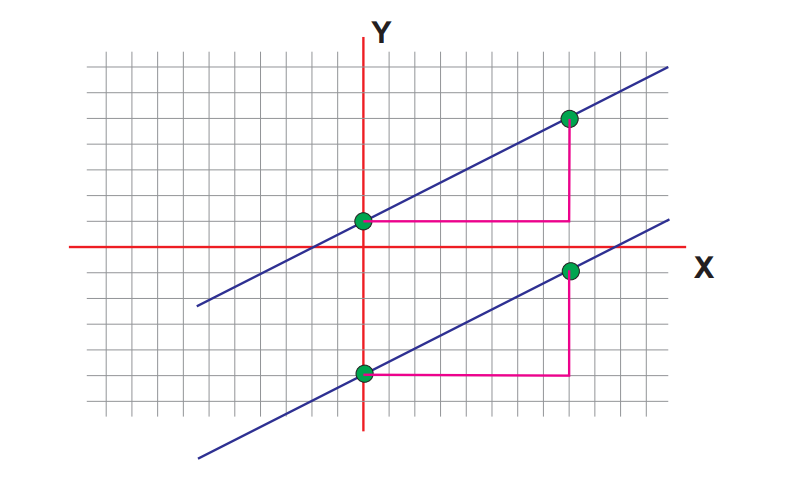
Si observamos las gráfcas en el sistema cartesiano podemos ver que a simple vista que estas rectas son paralelas. Ya que nunca se va a cortar entre sí.
Si buscamos la ecuación que las define nos encontramos con que:
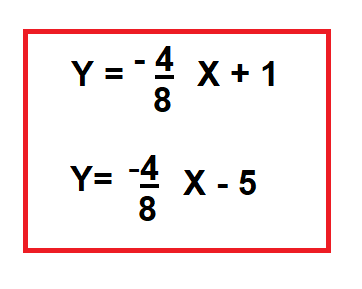
En base a los valores encontrados podemos decir que dos rectas son paralelas cuando tienen la misma pendiente.
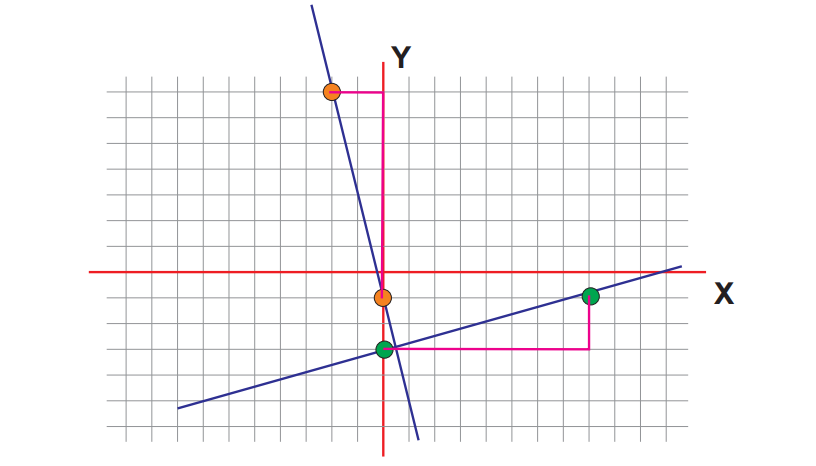
En esta situación, si observamos la gráfica podemos ver que son dos rectas perpendiculares. Pues, forman una cruz o 4 ángulos rectos.
El valor de cada recta es de:
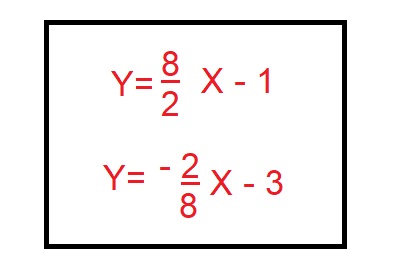
En base a los valores obtenidos, podemos decir que dos rectas son perpendiculares cuando sus pendientes son opestas e inversas.